Everything you want to know about mazes but you are afraid to ask
Wiktor Zychla
Maze created with TorqMaze 0.02
Download source and binaries of TorqMaze 0.02 (C#)
Download source and binaries of TorqMaze 0.01 (C#)
If you have any questions or comments about this article:
mail me.
How can we build mazes fast and efficiently?
How can we find a way through a maze fast and efficiently?
I've dediced to spend a few days for these problems
and this short article is the outcome of my research.
Maze generation
Maze generation algorithm is very intuitive. We start from a layout that has walls between all cells.
I will call such layout a foundation layout or just a foundation.
An algorithm consists in walking through the foundation and deciding whether a wall could be
removed. That's why it is really fast, it works in linear time.
Let's make a fast summary. The algorithm:
- walks through the foundation layout in a random way
- at each step it decides if the wall that separates cells can be removed
Walking through the foundation layout in a random way
This could be easily achieved with simple recursion:
walk_layout( x, y )
{
if ( visited( x, y ) ) return;
create_random_permutation( p )_of_a_set_0_3
call_with_the_sequence_determined_by_p
{
walk_layout( x-1, y );
walk_layout( x+1, y );
walk_layout( x, y-1 );
walk_layout( x, y+1 );
}
}
This, alas, will not work for big foundations because the stack is limited. In practice, with C# I failed
to create a 64x64 maze because I got an obvious exception "Stack overflow".
I solved this problem with iterative version of this algorithm. It required to implement a stack that would be
used while walking to store the current position and a value saying which directions had been already tried.
For example, if we are in cell (4, 5) and we walk to cell (4, 6) then we push to stack
(4, 5, directions | direction.E).
If we reach a cell and we see that all directions were already checked,
we just pop the state from the stack and try different ways for this state.
Removing walls while walking through the foundation
The second problem with maze generation is the necessity to check if two cells are already connected.
It is important because every two cells should be connectned with exactly one path.
If source and destination cells are connected then the algorithm aborts to remove the wall between them.
In practice this is not so simple to check if there is already a path between two cells.
Naive implementation would analyze whole maze generated to this moment!
I've decided to use a version of an algorithm said to be by Robert E. Tarjan.
I found a paper about it but it still looked quite messy and unnecessary complicated.
I've decided to simplify it.
This is the idea: in addidional table (called table of bases)
we store the information on connections between cells.
We will refer this table by a cell index ( index(X, Y) = maze_width * Y + X )
and the table will hold two types of data:
- the number -1 - means that the cell is a tail of a chain of connected cells
- positive number - means a pointer, a number of next cell in a chain you have to refer
Let's connect three cells (0, 0), (0, 1) and (0, 2) into one chain.
We count the indexes:
index(0, 0)=0, index(0, 1)=1, index(0, 2)=2
The table of bases will look like this:
[0] : -1
[1] : 0
[2] : 1
...
To compute the base cell of any given cell, we compute its index and then we search
the table of bases until we reach the tail
(code from TorqMaze 0.01):
int base_cell( int tIndex )
{
int index = tIndex;
while ( maze_base[ index ] >= 0 )
{
index = maze_base[ index ];
}
return index;
}
Then if we would like to check if two cells C1 i C2 are conencted we just compute thier base cells.
If base cells are equal then C1 and C2 are in the same chain.
This is because two separated chains can be merged together to form a new chain. We do this
by changing the base pointer of one chain:
void merge( int index1, int index2 )
{
// merge both lists
int base1 = base_cell( index1 );
int base2 = base_cell( index2 );
maze_base[ base2 ] = base1;
}
For example two separated chains
[0] : -1
[1] : 0
[2] : 1
and
[3] : -1
[4] : 3
[5] : 4
will be merged as:
[0] : -1
[1] : 0
[2] : 1
[3] : 0
[4] : 3
[5] : 4
Notice that base_cell() for each cell in this chain is equal to 0 and this means
that all cells are in one chain.
Combining of maze walking with removing of walls
Both parts of the maze algorithm are done in one pass. I remove a wall if it does not produce a cycle
in the maze. I store the wall info in special data structures.
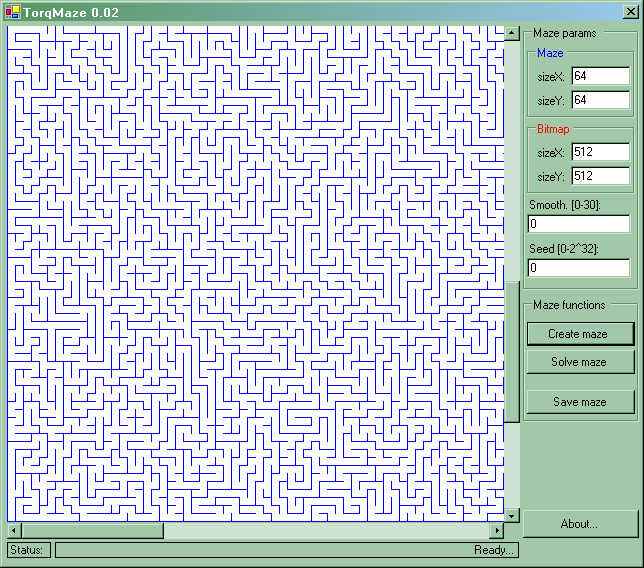
Interface of TorqMaze 0.01
Path finding
There are a lot of tricky algorithms for path finding in mazes.
I will present one of the most reliable but quite memory demanding
(it requires a temporary table as big as the maze)
The algorithm is quite simple.
I will provide an example:

In that temporary tablie (let's call it mazePath) we will build an image
of the path between source and destination point.
At the beginning we'll fill the table with -1.
| -1 | -1 | -1 | -1 |
| -1 | -1 | -1 | -1 |
| -1 | -1 | -1 | -1 |
| -1 | -1 | -1 | -1 |
We start by putting the value of 0 into the source point.
| 0 | -1 | -1 | -1 |
| -1 | -1 | -1 | -1 |
| -1 | -1 | -1 | -1 |
| -1 | -1 | -1 | -1 |
Then we do an i-step until we reach the destination point:
- all points that are neighbours to points filled in previous step
and are not filled yet should be filled with the value of i
only if we follow the maze
(we are not allowed to go through the walls)
The interpretation is simple - in i
-step we mark fields that are reachable with ... i steps.
Let's look at the example:
| 0 | 1 | -1 | -1 |
| -1 | -1 | -1 | -1 |
| -1 | -1 | -1 | -1 |
| -1 | -1 | -1 | -1 |
| 0 | 1 | -1 | -1 |
| -1 | 2 | -1 | -1 |
| -1 | -1 | -1 | -1 |
| -1 | -1 | -1 | -1 |
| 0 | 1 | -1 | -1 |
| 3 | 2 | 3 | -1 |
| -1 | 3 | -1 | -1 |
| -1 | -1 | -1 | -1 |
...we can reach 3 fields in 3 steps...
...
| 0 | 1 | -1 | -1 |
| 3 | 2 | 3 | -1 |
| 4 | 3 | 8 | -1 |
| 5 | 6 | 7 | 8 |
...and we reach the dest point in 8 steps!
At this time the first part of the algorithm is finished.
The only thing that we have to do is to build the path.
To do it we follow the consecutive numbers from 8 to 0, starting at the destination point
and ending at start point.
The path is ready.

All the details of the implementation can be found in the source of TorqMaze 0.02.
As the excercise, you should try this algorithm with more complicated mazes.




